回溯算法(Backtricking)
回溯逻辑部分一般存在递归函数下面
解决那些问题
组合问题
Eg: 给定 {1,2,3,4} 集合, 找到大小为2的组合。
切割问题
Eg:给定一串字符串,特定条件下,问有几种切割的方式。
子集问题
Eg: 给定 {1,2,3,4} 集合,找到它的所有子集。
排列问题
Eg: 讲顺序的组合问题
棋盘问题
Eg: N-Queen 和 解数独
Tips
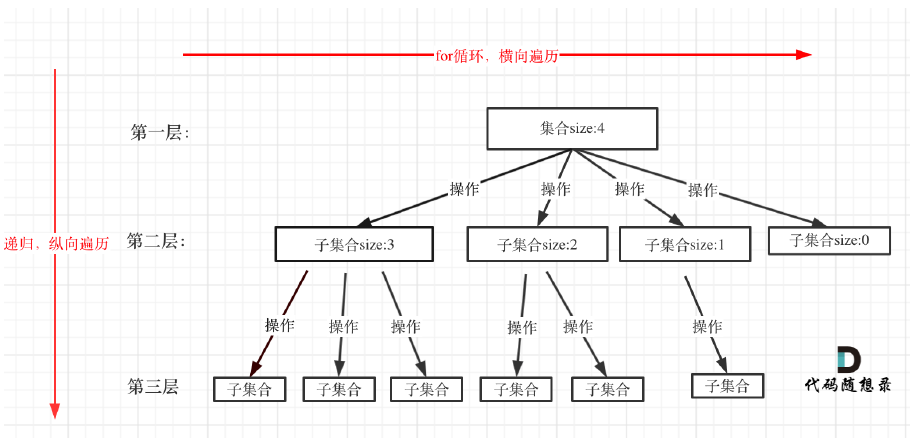
把回溯法问题最好抽象成图形结构,比如树结构。更好的方便理解。
树的宽度,就是处理问题集合的大小。 这里通常用for循环遍历
树的深度,就是递归函数的深度。 这里就是递归函数处理

回溯就是递归的过程
递归就一定有终止条件。
在这里递归函数没有返回值
模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14public void backtricking(parameters){
//递归终止 和 收集结果
if(终止条件){
// 收集结果
return;
}
//单层搜索逻辑
//for循环 处理集合里每一个搜索元素,树中节点孩子的数量就是集合大小
for(本层集合元素集){
// 根据条件 处理节点 以便于在满足终止条件时收集结果。
// 递归过程 backtricking(parameters)
// 回溯操作,撤销上一步处理节点的情况。比如: {1,2} 要把2 弹出去重新变成{1} 才能允许3再加进去。
}
}
刷题总结:
组合问题
17. Letter Combinations of a Phone Number